1. Galois Field (GF) Algebra

A field is a set of elements in which we can do addition, subtraction, multiplication, and division without leaving the set. The #elements in a field is called the order of the field.

GF algebra operates within a finite field, i.e. finite #elements.

1.1 Binary Field $GF(2)$

$G=\{0, 1\}$

The additive identity of an element is that element itself: subtraction in $GF(2)$ is equivalent to addition in $GF(2)$.

1.2 Extension Fields $GF(2^m)$

An extension field can be created by creating a primitive polynomial $p(x)$; once a $p(x)$ is found, then the elements of the Galois field can be generated. Any primitive polynomial $p(x)$ can construct the $P^m=2^m$ unique elements including a $0$ element and a $1$ element, i.e. $0,1,\alpha,\alpha^2, ... , \alpha^{n-1}$.

• Primitive polynomials $p(x)$

  $p(x)$ is defined to be an irreducible binary polynomial of degree $m$ which divides $X^n+1$ for $n=P^m-1=2^m-1$ and which does not divide $X^i+1$ for $i<n$.

• Field symbols $\alpha^i$

  Suppose we have a primitive polynomial $p(X)=X^4+X+1$ of degree $m=4$, we can now generate Galois field $GF(P^m)=GF(2^m)=GF(2^4)=GF(16)$.

  $\alpha^i = \alpha(X)\; mod\; F(X)=(i_3X^3+i_2X^2+i_1X+i_0)\; mod\; F(X)$

  There is one and only one $GF(2^m)$ for each $m$. However, there are many implementations for each $GF(2^m)$.

  • Case 1: $\alpha(X)=i_3X^3+i_2X^2+i_1X+i_0=\alpha=X$:

    $\alpha^{-inf}=0, \alpha^0=1$

    $\alpha^1=X, \alpha^2=\alpha\cdot\alpha=X\cdot X=X^2, \alpha^3=\alpha\cdot \alpha^2=X\cdot X^2=X^3$

    $\alpha^4=\alpha\cdot \alpha^3=X\cdot X^3=X^4=X^4\; mod\; F(X), F(X)=X^4+X+1=0, X^4=-X-1=X+1$

  • Case 2: $\alpha(X)=i_3X^3+i_2X^2+i_1X+i_0=\alpha=X^2$

    $\alpha^1=X2, \alpha^2=\alpha\cdot \alpha=X^2\cdot X^2=X^4\; mod\; F(X)=X+1$

    $\alpha^3=\alpha\cdot \alpha^2=X^2(X+1)=(X^3+X^2)\; mod\; F(X)$

    

2. RS Encoding

RS codes are BCH codes which are a subset of cyclic block codes. Cyclic block codes are a subset of linear block codes which are a subset of block codes which are a subset of error correction codes in general.

A RS code is specified as $RS(n, k)$ with $m$-bit symbols. This means that the encoder takes $k$ data symbols of $m$ bits each and adds parity symbols to make an $n$ symbol codeword. There are $n-k$ parity symbols of $m$ bits each. A RS decoder can correct up to $t$ symbols that contain errors in a codeword, where $2t=n-k$.

The code word $C(X)$ that we will transmit is comprised of $CK(X)$ appended systematically onto $M(X)$, $C(X)=X^{n-k}M(X)+CK(X)=X^{n-k}M(X) + X^{n-k}M(X)\; mod \; g(X)$

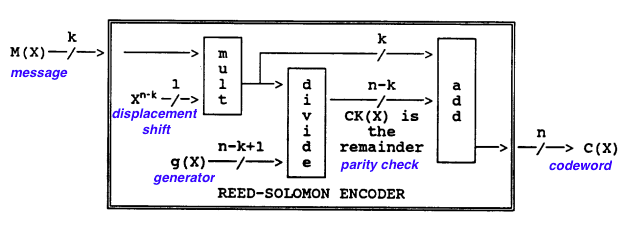
2.1 Generator polynomial $g(X)$

$g(X)_{RS\_code} = \prod_{i=FCR}^{FCR+2t-1}(X+(\alpha^G)^i)$

• FCR: the power of the first consecutive root in $g(X)$
• $\alpha^G$: any primitive element of $F(X)$

Suppose we select the code word generator's roots to be consecutive powers of $\alpha^G=\alpha^1=\alpha$, and we also start at $FCR=1$, then we get:

$\color{red}g(X)=\prod_{i=1}^{2t}(X+\alpha^i)=(X+\alpha)(X+\alpha^2) ... (X+\alpha^{2t}) = X^6+\alpha^{10}X^5+\alpha^{14}X^4+\alpha^4X^3+\alpha^6X^2+\alpha^9X+\alpha^6$

2.2 Code word polynomial $C(X)$

Now since we have determined our generator $g(X)$, we can construct $CK(X)$. Then we can append our message field $M(X)$ to it and thus construct our systematic code word $C(X)$.

Example: $M(X)=0X^8+0X^7+0X^6+0X^5+0X^4+0X^3+0X^2+\alpha^{11}X+0=\alpha^{11}X$, which represents the message $[0000000\alpha^{11}0]$, i.e., the binary symbol sequence "0000 0000 0000 0000 0000 0000 0000 1110 0000".

$C(X)=X^{n-k}M(X)+(X^{n-k}M(X))\; mod \;g(X)=(X^6)(\alpha^{11}X)+(X^6(\alpha^{11}X))\; mod \; g(X)=(\alpha^{11}X^7) + (\alpha^{11}X^7)\; mod \;g(X)$

$CK(X)=\alpha^{11}X^7\; mod \;g(X) =\alpha^8X^5+\alpha^{10}X^4+\alpha^4X^3+\alpha^{14}X^2+\alpha^8X+\alpha^{12}$

$C(X)=\alpha^{11}X^7 + CK(X)=\alpha^{11}X^7+ \alpha^8X^5+\alpha^{10}X^4+\alpha^4X^3+\alpha^{14}X^2+\alpha^8X+\alpha^{12}$

Putting together, $RS(15, 9)$ encodes the 9-symbol message by systematically adding 6-symbol redundancy:

$M(X)$ data: $\color{blue} 0000\; 0000\; 0000\; 0000\; 0000\; 0000\; 0000\; 1110\; 0000$

$C(X)$ data: $\color{blue} \;0000\; 0000\; 0000\; 0000\; 0000\; 0000\; 0000\; 1110\; 0000\; |\; 0101\; 0111\; 0011\; 1001\; 0101\; 1111$

3. RS Decoding

The decoding process is a 5-stage process:

• calculate the syndrome components from the received word;
• calculate the error-locator word from the syndrome components;
• calculate the error locations from the error-locator numbers which are from the error-locator word;
• calculate the error values from the syndrome components and the error-locator numbers;
• calculate the decoded code word from the received word, the error locations, and the error values.

Received word $R(X)$ consisting of received symbols $R_i$, which is the original (transmitted) codeword $C(X)$ plus errors $E(X)$:

$\color{red} R(X)=C(X)+E(X)=[(C_{n-1}+E_{n-1})X^{n-1} + (C_{n-2}+E_{n-2})X^{n-2} + ... + (C_1+E_1)X+(C_0+E_0)]$

To simply,

$R(X)=R_{n-1}X^{n-1}+R_{n-2}X^{n-2}+ ... + R_1X+R_0$

In Section 2, we get that

$C(X)=\alpha^{11}X^7+ \alpha^8X^5+\alpha^{10}X^4+\alpha^4X^3+\alpha^{14}X^2+\alpha^8X+\alpha^{12}$

Suppose that the received code word is

$R(X) = \underline{X^8} + \alpha^{11}X^7+ \alpha^8X^5+\alpha^{10}X^4+\alpha^4X^3+\underline{\alpha^{3}}X^2+\alpha^8X+\alpha^{12}$

Note that the coefficients of $X^8$, part of the RS data source field $[X^{n-k}M(X)]$, and $X^2$, part of the RS check symbol field $[X^{n-k}M(X)\; mod \;g(X)]$, has changed from $0$ and $\alpha^{14}$ to 1 and $\alpha^3$, respectively.

$R(X)$ data: $\color{blue} \;0000\; 0000\; 0000\; 0000\; 0000\; 0000\; \underline{0001}\; 1110\; 0000\; |\; 0101\; 0111\; 0011\; \underline{1000}\; 0101\; 1111$

3.1 Syndromes calculation

A RS codeword has $2t$ syndromes that depend only on errors (NOT on the transmitted codeword). We can get the syndromes by evaluating the received code polynomial at the values of $\alpha$ that are the roots of the generator, i.e., $\alpha^1, \alpha^2, ... , \alpha^{2t}$:

$\color{red} S_j=R(\alpha^j),\; j=1,2, ... , 2t$

Thus, we get

$S_1=R(\alpha^1)= (\alpha)^8 + \alpha^{11}(\alpha)^7 + \alpha^8(\alpha)^5 + \alpha^{10}(\alpha)^4 + \alpha^4(\alpha)^3 + \alpha^3(\alpha)^2 + \alpha^8(\alpha) + \alpha^{12} = 1$

$S_2=R(\alpha^2)=1$

$S_3=R(\alpha^3)=\alpha^5$

$S_4=R(\alpha^4)=1$

$S_5=R(\alpha^5)=0$

$S_6=R(\alpha^6)=\alpha^{10}$

3.2 Find an error-locator polynomial $\sigma(X)$

Error pattern $E(X)'$ consists of error locations $x_i$ and error values $y_i$:

$\color{red} E(X)'=y_1x_1 + y_2x_2 + ... + y_Tx_T$

$\sigma(X)$: error-locator polynomial where the inverse of its roots yield the error-locator numbers (or error-location) $z_i$;

$\sigma_r(X)$: the reciprocal of the error-locator polynomial $\sigma(X)$ where the roots of $\sigma_r(X)$ yield the error-locator numbers $z_i$.

The syndrome components $S_i$ are known; the error locations $x_i$ and the error values $y_i$ are unknown. The $S_i$ is related to the $z_i$ (i.e., also the $x_i$) and the $y_i$ by the following set of independent NON-LINEAR equations called weighted power-sum symmetric functions.

$\color{red} S_i = \sum_{j=1}^{T}y_jz_j^i, \;\;i=FCR, FCR+1, ..., 2t+FCR-1; \; T\;is\#errors$

Usually there are many solutions to the above set of NON-LINEAR equations; these solutions are within a distance of $t$ errors. However, there is always only one correct solution within a distance of $t$ symbols; the correct solution is simply the $\sigma_r(X)$ polynomial representing the fewest errors (i.e., the lowest psbl value of $T$) occurring.

Once $\sigma_r(X)$ is known, the error locations $x_i$ can be determined and the the equation simplifies into a standard set of independent LINEAR equations. We can then solve these LINEAR equations for the $y_i$.

Let $\color{red} S(X)=\sum_{i=1}^{2t}S_iX^{i-1}=S_1 + S_2X + ... + S_5X^4 + S_6X^5=\alpha^{10}X^5 + X^3 + \alpha^5X^2 + X + 1$

Divide $X^{2t}$ by $S(X)$, then $S(X)$ by $r_1$, $r_1$ by $r_2$, $r_2$ by $r_3$, ... , until the degree of $r_i \le t$:

• divide $X^6$ by $S(X)$: $\frac{X^6}{S(X)}=\alpha^5X + \frac{\alpha^5X^4+\alpha^{10}X^3+\alpha^5X^2+\alpha^5X}{S(X)}$

  $X^6 = (\alpha^5X)S(X) + (\alpha^5X^4+\alpha^{10}X^3+\alpha^5X^2+\alpha^5X)$

  $X^6 = (q_1\;\;\;\;)S(X) + (r_1)$

  $r_1 = \alpha^5X^4+\alpha^{10}X^3+\alpha^5X^2+\alpha^5X$, the degree of $r_1 = 4 > t=3$

• divide $S(X)$ by $r_1$: $\frac{S(X)}{r_1}=\alpha^5X + \alpha^{10} + \frac{1}{r_1}$

  $S(X)=(\alpha^5X + \alpha^{10})r_1 + 1$

  $S(X) = (q_2)r_1 \;\;\;\;\;\;\;\;\;\;+ r_2$

  $r_2=0 \le t=3$. STOP !!!

Put the previous results into the following form:

$\color{red} S(X)\sigma(X) = A(X) + X^{2t}B(X)$

A summary of the previous results is:

$r_1 = X^6 + q_1S(X)$

$r_2 = S(X) + q_2r_1$

Combining to form one equation:

$r_2 = S(X) + q_2[X^6 + q_1S(X)] = X^6[q_2] + S(X)[1+q_1q_2]$

Substituting values:

$1 = X^6[\alpha^5X + \alpha^{10}] + S(X)[1 + (\alpha^5X)(\alpha^5X + \alpha^{10})]$

$\;\;\;= X^6[\alpha^5X + \alpha^{10}] + S(X)[\alpha^{10}X^2 + X + 1]$

Put in proper form of $S(X)\sigma(X) = A(X) + X^{2t}B(X)$:

$S(X)[\alpha^{10}X^2 + X + 1] = 1 + X^6[\alpha^5X+10]$

Thus, the error-locator $\sigma(X) = \alpha^{10}X^2 + X + 1 = \sigma_2X^2 + \sigma_1X + 1$

Therefore, $\sigma_1=1$ and $\sigma_2=a^{10}$

$\sigma_r(X) = X^T\sigma(X^{-1}) = X^2(1+X{-1}+\alpha^{10}X^{-2}) = X^2 + X + \alpha^{10}$

3.3 Error locations $x_i$ (Find the roots of $\sigma(X)$)

We find the error locations $x_i$ by first finding the error-locator numbers $z_i$. The $z_i$ are the roots of $\sigma_r(X)$ or are the inverse of the roots of $\sigma(X)$. There are two equivalent algorithms to find the error locations $x_i$. They are the Chien search and explicit factorization, which both find the roots in the error-locator.

The Chien search calculates the outputs for all the possible inputs; it is a very simple, brute force, search algorithm. The roots of the reciprocal of the error-locator polynomial $\sigma_r(X)$ are the error-locator numbers $z_i$.

$\color{red} \sigma_r(X) = \prod_{i=1}^{i=T}(X+z_i), \;\; for\; z_i\; in\; the\; form\; of\; \alpha^j$

Find the roots of $\sigma_r(X)$, i.e., determine $\sigma_r(X)=0$ for $X=1, \alpha, \alpha^2, ... , \alpha^{n-1}$

$\sigma_r(X) = X^2 + X + \alpha^{10}$

$\sigma_r(1) = (1)^2 + (1) + \alpha^{10} = 1 +\alpha^5 = \alpha^{10}$

$\sigma_r(\alpha) = (\alpha)^2 + (\alpha) + \alpha^{10} = \alpha^2 + \alpha^8 = 1$

$\sigma_r(\alpha^2) = (\alpha^2)^2 + (\alpha^2) + \alpha^{10} = \alpha^4 + \alpha^4 = 0$

$\sigma_r(\alpha^3) = \alpha^6 + \alpha^{12} = \alpha^4$

$\sigma_r(\alpha^4) = \alpha^8 + \alpha^{2} = 1$

$\sigma_r(\alpha^5) = \alpha^{10} + 1 = \alpha^5$

$\sigma_r(\alpha^6) = \alpha^{12} + \alpha^7 = \alpha^2$

$\sigma_r(\alpha^7) = \alpha^{14} + \alpha^{6} = \alpha^8$

$\sigma_r(\alpha^8) = \alpha + \alpha = 0$

$\sigma_r(\alpha^9) = \alpha^8$, $\sigma_r(\alpha^{10}) = \alpha^5$, $\sigma_r(\alpha^{11}) = \alpha$, $\sigma_r(\alpha^{12}) = \alpha$, $\sigma_r(\alpha^{13}) = \alpha^2$, $\sigma_r(\alpha^{14}) = \alpha^4$

The two error-locator (or error location) numbers are $z_1=\alpha^2$ and $z_2=\alpha^8$, which leads to $\sigma_r(X)=0$.

The Chien search results of $x_1=X^2$ and $x_2=X^8$ checks with the code word.

3.4 Find the symbol error values $y_i$

Since $T$, $x_i$, and $S_i$ are known, we can solve the set of linear equations for $y_i$

$\color{red} S_i = \sum_{j=1}^{T}y_jz_j^i, \;\;i=FCR, FCR+1, ..., 2t+FCR-1; \; T\;is\#errors$

For the example here, these weighted power-sum symmetric functions reduce to:

$S_i = \sum_{j=1}^2y_jz_j^i, \;\; where\; i=1,2,...,6\; and\; where\; T=2$

We can get:

$y_1(z_1) + y_2(z_2) = S_1$

$y_1(z_1)^2 + y_2(z_2)^2 = S_2$

$y_1(z_1)^3 + y_2(z_2)^3 = S_3$

$y_1(z_1)^4 + y_2(z_2)^4 = S_4$

$y_1(z_1)^5 + y_2(z_2)^5 = S_5$

$y_1(z_1)^6 + y_2(z_2)^6 = S_6$

We only need $T=2$ of these equations since we have $T=2$ unknowns (i.e., $y_1$ and $y_2$). Pick two equations:

$y_1(z_1) + y_2(z_2) = S_1$

$y_1(z_1)^2 + y_2(z_2)^2 = S_2$

Substitute $z_1=\alpha^2$ and $z_2=\alpha^8$ to transform the preceding set into the following linear set:

$y_1(\alpha^2) + y_2(\alpha^8) = 1$

$y_1(\alpha^2)^2 + y_2(\alpha^8)^2 = 1$

This simplifies to:

$y_1\alpha^2 + y_2\alpha^8 = 1$

$y_1\alpha^4 + y_2\alpha = 1$

We can easily get that $y_1=1$ and $y_2=1$.

3.5 Decoded code word $C(X)'$

Now since we have already calculated all our error locations $x_i$ and error values $y_i$, we have just finished constructing our estimate of the error $E(X)'$ which is simply the estimate of the noise.

$\color{red} E(X)' = \sum_{i=1}^Ty_ix_i = y_1x_1 + y_2x_2 = (1)(X^2) + (1)(X^8) = X^2 + X^8$

As $R(X) = C(X) + E(X)$, and the decoder only has the received vector $R(X)$ and the estimated error $E(X)'$, the closest code word $C(X)'$ can be determined as a function of $R(X)$ and $E(X)'$:

$\color{red} C(X)' = R(X) - E(X)' = R(X) + E(X)'$

$C(X)' = R(X) + E(X)' = [\underline{X^8} + \alpha^{11}X^7+ \alpha^8X^5+\alpha^{10}X^4+\alpha^4X^3+\underline{\alpha^{3}}X^2+\alpha^8X+\alpha^{12}] + [X^8+X^2]$

$C(X)' = \alpha^{11}X^7 + \alpha^8X^5 + \alpha^{10}X^4 + \alpha^4X^3 + \alpha^{14}X^2 + \alpha^8X + \alpha^{12}$

$C(X)'$ is indeed the same as $C(X)$.

Now strip the message field from the corrected data:

$X^{n-k}M(X)' = \alpha^{11}X^7,\; where n=15,\; k=9$, and thus $M(X)'=\alpha^{11}X$

References

[1]. [Tutorial on Reed-Solomon error correction coding][http://jeffareid.net/misc/msc-21834.pdf]

[2]. [Reed-Solomon codes'1][https://www.cs.cmu.edu/~guyb/realworld/reedsolomon/reed_solomon_codes.html]

[3]. [Decoding BCH codes][http://ocw.usu.edu/Electrical_and_Computer_Engineering/Error_Control_Coding/lecture7.pdf]

[4]. [Notes on Reed-Solomon codes][https://math.berkeley.edu/~mhaiman/math55/reed-solomon.pdf]

[5]. [Reed-Solomon codes'2][https://www.cs.duke.edu/courses/spring10/cps296.3/rs_scribe.pdf]

[6]. [Implementing Reed-Solomon][https://www.cs.duke.edu/courses/spring11/cps296.3/decoding_rs.pdf]

[7]. [BCH, Reed-Solomon, and related codes][http://www.work.caltech.edu/~ling/webs/EE127/EE127A/handout/Ch9.pdf]